k strain hydraulic|Hydraulic Conductivity (K) : department Store All hydraulic applications are based on flow and pressure requirements. Flow, expressed in gallons per minute (GPM), determines the speed at which a hydraulic cylinder extends or a . Bem-vindo a VegasSlotsOnline. Mais de 10.000 slots para jogar GRÁTIS. Mais de 1.200 casinos avaliados. Mais de 1 milhão de visitantes mensalmente. Jogue nas Nossas Slots GRÁTIS Jogue em Slots a Dinheiro Real. As Melhores Slots de Vegas Online. Obtenha uma experiência digna de Vegas com as melhores slots.
{plog:ftitle_list}
WEB2 de jun. de 2023 · Tabelas, fichas de jogo e estatísticas sobre competições, jogadores e treinadores, tanto do futebol brasileiro quando do futebol internacional. . Botafogo-SP e Tombense não saem do zero O Botafogo-SP e o Tombense empataram em 0 a 0, na noite desta sexta-feira, 2, .
The calculation has four components: strain-stress data from a step-load test; one-dimensional vertical consolidation theory relating K s a t to the coefficient of consolidation; the relation .
Hydraulic conductivity, sometimes called permeability, expresses how fast water flows through the soil voids; it is a function of the texture, grain size and distribution, density, as well as the .
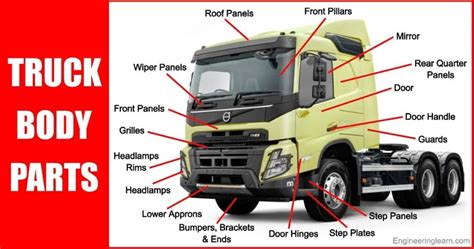
UNDERSTANDING TRUCK
Propagation of a plane
“Hydraulic Conductivity” (K), in hydrogeology and hydrology, represents the capacity of a porous medium (such as soil) to transmit water, as per Darcy’s Law.All hydraulic applications are based on flow and pressure requirements. Flow, expressed in gallons per minute (GPM), determines the speed at which a hydraulic cylinder extends or a .k = hydraulic conductivity, ft/s or m/s. Additional Resources. Duffield, G. (2019, June 06). Aquifer testing 101: Hydraulic properties representative values of hydraulic properties. Retrieved . Significant efforts have been expended for improved characterization of hydraulic conductivity (K) and specific storage (Ss) to better understand groundwater flow and .
This paper studies the propagation of a plane-strain fluid-driven fracture with a fluid lag in an elastic solid. The fracture is driven by a constant rate of injection of an incompressible . This paper develops an approximate solution for the problem of a plane strain hydraulic fracture that is driven by a Newtonian fluid and propagates in a permeable medium . Following the theory proposed by Snow [3], a strain-dependent equivalent hydraulic conductivity tensor for fractured rock masses with n sets of fractures is represented by (39) K = ∑ f k f (δ-n f ⊗ n f) = ∑ f k f 0 1 + s f b f 0 Δ ɛ zf 3 (δ-n f ⊗ n f), where K is the equivalent hydraulic conductivity tensor of the examined rock mass . Summary. Low‐frequency distributed acoustic‐sensing (LF‐DAS) data are promising attributes for detecting fracture hits and fracture characterization. However, measured signals from different wells exhibiting various characteristics and mechanisms attributing to the difference are not well understood, which makes the interpretation of field LF‐DAS data most .
In the language of physics, two terms describe the forces on objects undergoing deformation: stress and strain. Stress is a quantity that describes the magnitude of forces that cause deformation. Stress is generally defined as force per unit .Bulkhead Hydraulic Hose Strain Relief Kits See Product Details Advice & How-To. 3.1 out of 5 Customer Rating Model # P015921091 Mfg # .99 Price reduced from to See Product Details Advice & How-To. 3.1 out of 5 Customer Rating Model # P015921091 Mfg # Select a . In this paper, we investigate the growth of a finite plane-strain hydraulic fracture from nucleation to the late stage of growth accounting for the presence of both a cohesive zone and a fluid lag. We also investigate the impact of a decreased hydraulic conductivity in the rough cohesive zone using existing phenomenological approximations.
This paper studies the propagation of a plane-strain fluid-driven fracture with a fluid lag in an elastic solid. The fracture is driven by a constant rate of injection of an incompressible viscous .ABSTRACT Hydraulic fracturing operations in unconventional reservoirs are typically monitored using geophones located either at the surface or in the adjacent wellbores. A new approach to record hydraulic stimulations uses fiber-optic distributed acoustic sensing (DAS). A fiber-optic cable was installed in a treatment well in the Meramec formation to monitor the hydraulic .Abstract We modeled cross-well strain/strain rate responses of fiber optic sensing, including distributed strain sensing (DSS) and low-frequency distributed acoustic sensing (DAS), to hydraulic stimulation. DSS and low-frequency DAS have been used to measure strain or the strain rate to characterize hydraulic fractures. However, the current application of DSS/DAS .
Calculation of the Saturated Hydraulic Conductivity of Fine-Grained Soils is the fourth standard in a series that enhances the probabilistic characterization and understanding of the behavior of a key . strain-stress data from a step-load test; one-dimensional vertical consolidation theory relating K s a t to the .All hydraulic applications are based on flow and pressure requirements. Flow, expressed in gallons per minute (GPM), determines the speed at which . a hydraulic cylinder extends or a hydraulic motor turns. Flow is produced by the pump. Pressure, expressed in pounds per square inch (PSI), determines the amount of force exerted. The above discussion highlights one of the main quandaries of devising a robust algorithm for predicting the evolution of plane strain hydraulic fractures when K m is small (say ≲1). As it will be made clear below, the presence of a sizeable lag region exists only for small K m and for time small compared to a characteristic time t om = E . The model considers a straight, plane strain hydraulic fracture (HF) characterized by the fracture half-length, l (t), and aperture, w (x, t), where x is the spatial coordinate (Fig. 1).The compressible fluid is injected at a constant rate, Q 0, to drive the fracture through a permeable rock.The pressure inside the fracture, p f (x, t), is the sum of the net pressure, p (x, t), .
Hydraulic Permeability
An approximate solution for a plane strain hydraulic fracture that accounts for fracture toughness, fluid viscosity, and leak-off. June 2017; International Journal of Fracture 205(2)This bulkhead strain relief fitting prevents kinks and chafing in hydraulic steering hoses, ensuring durability and leak-free performance. Available in black or chrome finishes, it protects hoses while accommodating specific size requirements.Hydraulic fractures are known to have a complex multiscale behavior even for the simplest cases of a semi-infinite, a finite plane strain (KGD), and a radial crack, see e.g. a thorough review paper (Detournay 2016). A semi-infinite hydraulic fracture is the model for the tip region of a hydraulic fracture [see (Peirce Summary. Low-frequency distributed-acoustic-sensing (LF-DAS) strain data are direct measurements of in-situ rock deformation during hydraulic-fracturing treatments. In addition to monitoring fracture propagation and identifying fracture hits, quantitative strain measurements of LF-DAS provide opportunities to quantify fracture geometries. Recently, we .
of a plane-strain hydraulic fracture in Fig. 1 via a triangu-lar phase diagram. The O-, M-, and K-vertex correspond respectively to the limiting case of a signicant lag/negli-gible toughness, the viscosity-dominated propagation with zero uid lag, and the toughness-dominated propagation Illustration of the growth of a plane-strain hydraulic fracture with the possible presence of a fluid lag and propagation schemes for a continuous injection and a fluid shut-in.
Boone and Ingraffea [10] presented an early work to simulate hydraulic fracturing using a fully-coupled 2D FEM model. More recently, many other more advanced 2D and 3D FEM models [14, 15, 16,48,64 .
Download scientific diagram | Geometry of the KGD (plane strain) hydraulic fracture. from publication: Toughness-dominated Hydraulic Fracture with Leak-off | This paper considers the problem of a .Glue these gauges onto a structure to measure strain in a single direction. Force Sensors. Tension and Compression Force Sensors. Also known as load cells, these sensors measure and track the forces of your equipment by converting them . Volume strain = \( \frac{ΔV}{V} \) Obviously, it is caused by external hydraulic pressure. Hooke’s Law. Hooke’s Law states that stress and strain are proportional to each other. That is, they have a linear relationship. That is, stress α strain Or stress = k × strain. where k is the proportionality constant and is known as modulus of . Summary. The use of fiber optics in reservoir surveillance is bringing valuable insights into fracture geometry and fracture-hit identification, stage communication, and perforation cluster fluid distribution in many hydraulic fracturing processes. However, given the complexity associated with field data, its interpretation is a major challenge faced by engineers .

The hydraulic bulge test, in combination with a digital image correlation (DIC) system, is the state of the art in the determination of biaxial stress-strain curves [8, 13,14]. However, there are . For two distinct hydraulic responses, various ways to delineate the fracture from the reservoir domain have been proposed. Mikelić et al. (2015a, 2015b) [14], [15] applied a Darcy flow in reservoir and a Poiseuille flow in fracture and relied on the phase-field value to transition between them. Another way to delineate the fracture was proposed by Wilson and Landis .Abstract Hydraulic fracturing operations in unconventional reservoirs are monitored using distributed fiber-optic sensing through which physical effects such as temperature, strain, and microseismic activity can be measured. When combined with treatment curves and other reservoir information, these measurements give engineers more data to understand the effectiveness of .
The Kristianovich-Geertsma-de Klerk (KGD) radial model is a classic 2D hydraulic fracturing model, named in honor of three researchers who contributed to it. The following assumptions are used in the model: The . with the plane strain Young’s modulus \(E' .
Hydraulic Conductivity Ranges of Various Soil Types

Hydraulic Conductivity (K)
Evaluation of Hydraulic Conductivity Estimates from Various
Determining flow stress of tubes
Resultado da Aposte na Zebra. 5.9K likes. Aposte na Zebra - A Casa da Loteca no Brasil – Excelência em Análises, Informações e Ferramentas Exclusivas Para a Loteca.
k strain hydraulic|Hydraulic Conductivity (K)